Virial expansion

The virial expansion is a model of thermodynamic equations of state. It expresses the pressure P of a gas in local equilibrium as a power series of the density. This equation may be represented in terms of the compressibility factor, Z, as $$Z\equiv {\frac {P}{RT\rho }}=A+B\rho +C\rho ^{2}+\cdots$$ This equation was first proposed by Kamerlingh Onnes. The terms A, B, and C represent the virial coefficients. The leading coefficient A is defined as the constant value of 1, which ensures that the equation reduces to the ideal gas expression as the gas density approaches zero.

Second and third virial coefficients

The second, B, and third, C, virial coefficients have been studied extensively and tabulated for many fluids for more than a century. Two of the most extensive compilations are in the books by Dymond and the National Institute of Standards and Technology's Thermo Data Engine Database and its Web Thermo Tables. Tables of second and third virial coefficients of many fluids are included in these compilations.

The 2nd and 3rd virial coefficients of argon

Casting equations of the state into virial form

Most equations of state can be reformulated and cast in virial equations to evaluate and compare their implicit second and third virial coefficients. The seminal van der Waals equation of state was proposed in 1873: $$P={\frac {RT}{\left(v-b\right)}}-{\frac {a}{v^{2}}}$$ where v = 1/ρ is molar volume. It can be rearranged by expanding 1/(v − b) into a Taylor series: $$Z=1+\left(b-{\frac {a}{RT}}\right)\rho +b^{2}\rho ^{2}+b^{3}\rho ^{3}+\cdots$$

In the van der Waals equation, the second virial coefficient has roughly the correct behavior, as it decreases monotonically when the temperature is lowered. The third and higher virial coefficients are independent of temperature, and are not correct, especially at low temperatures.

Almost all subsequent equations of state are derived from the van der Waals equation, like those from Dieterici, Berthelot, Redlich-Kwong, and Peng-Robinson suffer from the singularity introduced by 1/(v - b).

Other equations of state, started by Beattie and Bridgeman, are more closely related to virial equations, and show to be more accurate in representing behavior of fluids in both gaseous and liquid phases. The Beattie-Bridgeman equation of state, proposed in 1928, $$p={\frac {RT}{v^{2}}}\left(1-{\frac {c}{vT^{3}}}\right)(v+B)-{\frac {A}{v^{2}}}$$ where

• $A=A_{0}\left(1-{\frac {a}{v}}\right)$
• $B=B_{0}\left(1-{\frac {b}{v}}\right)$

can be rearranged as $$Z=1+\left(B_{0}-{\frac {A_{0}}{RT}}-{\frac {c}{T^{3}}}\right)\rho -\left(B_{0}b-{\frac {A_{0}a}{RT}}+{\frac {B_{0}c}{T^{3}}}\right)\rho ^{2}+\left({\frac {B_{0}bc}{T^{3}}}\right)\rho ^{3}$$The Benedict-Webb-Rubin equation of state of 1940 represents better isotherms below the critical temperature: $$Z=1+\left(B_{0}-{\frac {A_{0}}{RT}}-{\frac {C_{0}}{RT^{3}}}\right)\rho +\left(b-{\frac {a}{RT}}\right)\rho ^{2}+\left({\frac {\alpha a}{RT}}\right)\rho ^{5}+{\frac {c\rho ^{2}}{RT^{3}}}\left(1+\gamma \rho ^{2}\right)\exp \left(-\gamma \rho ^{2}\right)$$

More improvements were achieved by Starling in 1972: $$Z=1+\left(B_{0}-{\frac {A_{0}}{RT}}-{\frac {C_{0}}{RT^{3}}}+{\frac {D_{0}}{RT^{4}}}-{\frac {E_{0}}{RT^{5}}}\right)\rho +\left(b-{\frac {a}{RT}}-{\frac {d}{RT^{2}}}\right)\rho ^{2}+\alpha \left({\frac {a}{RT}}+{\frac {d}{RT^{2}}}\right)\rho ^{5}+{\frac {c\rho ^{2}}{RT^{3}}}\left(1+\gamma \rho ^{2}\right)\exp \left(-\gamma \rho ^{2}\right)$$

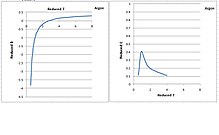
Following are plots of reduced second and third virial coefficients against reduced temperature according to Starling:

The 2nd and 3rd virial coefficients for 12 fluids

The exponential terms in the last two equations correct the third virial coefficient so that the isotherms in the liquid phase can be represented correctly. The exponential term converges rapidly as ρ increases, and if only the first two terms in its Taylor expansion series are taken, $1-\gamma \rho ^{2}$, and multiplied with $1+\gamma \rho ^{2}$, the result is $1-\gamma ^{2}\rho ^{4}$, which contributes a $c/RT^{3}$ term to the third virial coefficient, and one term to the eighth virial coefficient, which can be ignored.

After the expansion of the exponential terms, the Benedict-Webb-Rubin and Starling equations of state have this form: $$Z=1+b\rho _{r}+c\rho _{r}^{2}+f\rho _{r}^{5}$$

Cubic virial equation of state

The three-term virial equation or a cubic virial equation of state $$Z=1+B\rho +C\rho ^{2}$$ has the simplicity of the Van der Waals equation of state without its singularity at v = b. Theoretically, the second virial coefficient represents bimolecular attraction forces, and the third virial term represents the repulsive forces among three molecules in close contact.

With this cubic virial equation, the coefficients B and C can be solved in closed form. Imposing the critical conditions: $${\frac {\mathrm {d} P}{\mathrm {d} v}}=0\qquad {\text{and}}\qquad {\frac {\mathrm {d} ^{2}P}{\mathrm {d} v^{2}}}=0$$ the cubic virial equation can be solved to yield: $$B=-v_{c},$$ $$C={\frac {v_{c}^{2}}{3}},$$ and $$Z_{c}={\frac {P_{c}v_{c}}{RT_{c}}}={\frac {1}{3}}.$$ $Z_{c}$ is therefore 0.333, compared to 0.375 from the Van der Waals equation.

Between the critical point and the triple point is the saturation region of fluids. In this region, the gaseous phase coexists with the liquid phase under saturation pressure $P_{\text{sat}}$, and the saturation temperature $T_{\text{sat}}$. Under the saturation pressure, the liquid phase has a molar volume of $v_{\text{l}}$, and the gaseous phase has a molar volume of $v_{\text{g}}$. The corresponding molar densities are $\rho _{\text{l}}$ and $\rho _{\text{g}}$. These are the saturation properties needed to compute second and third virial coefficients.

A valid equation of state must produce an isotherm which crosses the horizontal line of $P_{\text{sat}}$ at $v_{\text{l}}$ and $v_{\text{g}}$, on $T_{\text{sat}}$. Under $P_{\text{sat}}$ and $T_{\text{sat}}$, gas is in equilibrium with liquid. This means that the PρT isotherm has three roots at $P_{\text{sat}}$. The cubic virial equation of state at $T_{\text{sat}}$ is: $$P_{\text{sat}}=RT_{\text{sat}}\left(1+B\rho +C\rho ^{2}\right)\rho$$ It can be rearranged as: $$1-{\frac {RT_{\text{sat}}}{P_{\text{sat}}}}\left(1+B\rho +C\rho ^{2}\right)\rho =0$$ The factor $RT_{\text{sat}}/P_{\text{sat}}$ is the volume of saturated gas according to the ideal gas law, and can be given a unique name $v^{\text{id}}$: $$v^{\text{id}}={\frac {RT_{\text{sat}}}{P_{\text{sat}}}}$$ In the saturation region, the cubic equation has three roots, and can be written alternatively as: $$\left(1-v_{\text{l}}\rho \right)\left(1-v_{\text{m}}\rho \right)\left(1-v_{\text{g}}\rho \right)=0$$ which can be expanded as: $$1-\left(v_{\text{l}}+v_{\text{g}}+v_{m}\right)\rho +\left(v_{\text{l}}v_{\text{g}}+v_{\text{g}}v_{\text{m}}+v_{\text{m}}v_{\text{l}}\right)\rho ^{2}-v_{\text{l}}v_{\text{g}}v_{\text{m}}\rho ^{3}=0$$ $v_{\text{m}}$ is a volume of an unstable state between $v_{\text{l}}$ and $v_{\text{g}}$. The cubic equations are identical. Therefore, from the linear terms in these equations, $v_{m}$ can be solved: $$v_{\text{m}}=v^{\text{id}}-v_{\text{l}}-v_{\text{g}}$$ From the quadratic terms, B can be solved: $$B=-{\frac {\left(v_{\text{l}}v_{\text{g}}+v_{\text{g}}v_{\text{m}}+v_{\text{m}}v_{\text{l}}\right)}{v^{\text{id}}}}$$ And from the cubic terms, C can be solved: $$C={\frac {v_{\text{l}}v_{\text{g}}v_{\text{m}}}{v^{\text{id}}}}$$ Since $v_{\text{l}}$, $v_{\text{g}}$ and $P_{\text{sat}}$ have been tabulated for many fluids with $T_{\text{sat}}$ as a parameter, B and C can be computed in the saturation region of these fluids. The results are generally in agreement with those computed from Benedict-Webb-Rubin and Starling equations of state.

See also

• Virial theorem
• Statistical mechanics
• Equation of state