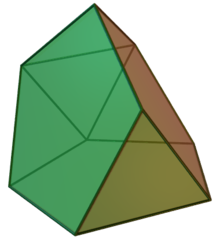
Tridiminished icosahedron

Tridiminished icosahedron
Type	Johnson J62 – J63 – J64
Faces	5 triangles 3 pentagons
Edges	15
Vertices	9
Vertex configuration	$2\times 3\times (3\times 5^{2})+3\times (3^{3}\times 5)$
Symmetry group	$C_{3\mathrm {v} }$
Properties	convex, non-composite
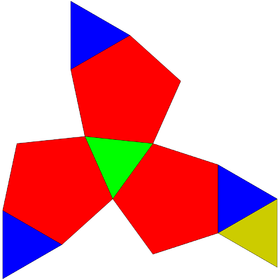
Net

In geometry, the tridiminished icosahedron is a Johnson solid that is constructed by removing three pentagonal pyramids from a regular icosahedron.

Construction

The tridiminished icosahedron can be constructed by removing three regular pentagonal pyramid from a regular icosahedron. The aftereffect of such construction leaves five equilateral triangles and three regular pentagons. Since all of its faces are regular polygons and the resulting polyhedron remains convex, the tridiminished icosahedron is a Johnson solid, and it is enumerated as the sixty-third Johnson solid $J_{63}$. This construction is similar to other Johnson solids as in gyroelongated pentagonal pyramid and metabidiminished icosahedron.

The tridiminished icosahedron is non-composite polyhedron, meaning it is convex polyhedron that cannot be separated by a plane into two or more regular polyhedrons.

Properties

The surface area of a tridiminished icosahedron $A$ is the sum of all polygonal faces' area: five equilateral triangles and three regular pentagons. Its volume $V$ can be ascertained by subtracting the volume of a regular icosahedron with the volume of three pentagonal pyramids. Given that $a$ is the edge length of a tridiminished icosahedron, they are: $${\begin{aligned}A&={\frac {5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}}{4}}a^{2}&\approx 7.3265a^{2},\\V&={\frac {15+7{\sqrt {5}}}{24}}a^{3}&\approx 1.2772a^{3}.\end{aligned}}$$

See also

• Snub 24-cell, a 4-polytope whose vertex figure is a tridiminished icosahedron

External links

• Weisstein, Eric W., "Tridiminished icosahedron" ("Johnson Solid") at MathWorld.